Public-Key Cryptography
이전 글에서 정리했던 HMAC, Sealed Box암호화는 Sender와 Receiver모두 키를 알고 있는 대칭키를 사용합니다.
대칭키는 대역 외(Out of band)로 전송되어야 하고, 이 작업을 안전하게 수행할 수 없는 경우 공개키 암호화(public-key cryptography)를 사용합니다. 실제로 인터넷에서 일상적으로 사용하는 대부분의 암호화는 공개키 암호화를 사용하고, Xcode가 앱에 서명을 할 때에도 동일합니다.
공개키 암호화는 수학적으로 연결된 두개의 키를 생성합니다. 개인키는 비밀로 유지하고 해당 공개키 Data를 게시합니다. 개인키로 Data 혹은 Data Digest에 서명한 다음 전송합니다. Receiver는 공개키 Data에서 공개키를 생성한 다음 이를 사용하여 Signed Data 혹은 Digest를 확인합니다.
예를 들어, 앱에서 백엔드 서버로 작업을 인증해야 할 수 있습니다. 사용자 디바이스에서 개인키를 생성해서 Keychain 혹은 SecureEnclave에 저장한 다음, 해당 공개키를 서버에 등록합니다. 사용자가 작업을 설정하면 앱이 사용자의 개인키로 작업 세부정보에 서명하고 서명된 세부정보를 서버로 전송하면 서버가 사용자의 공개키로 이를 확인합니다.
Encrypted data를 전송하려면 사용자와 Receiver가 각각 키 쌍을 생성하고 공개키를 게시합니다. 그리고 사용자, Receiver 모두 자신의 개인키와 상대방의 공개키를 결합해서 shared secret을 생성합니다. 양쪽 모두 이 shared secret을 사용하여 동일한 대칭키를 만들어낸 다음 위에서 설명했던 AEAD에 사용할 수 있습니다.
개인키, 공개키 생성하기
공개키 암호화의 주요 특징은 Trapdoor 알고리즘을 사용한다는 점입니다. 공개키로부터 개인키를 계산해내는 것은 매우 어렵습니다.
1978년 RSA(Rivest-Shamir-Adleman)가 발표된 후 가장 널리 사용되는 공개키 알고리즘이 되었습니다. RSA 알고리즘은 매우매우 큰 수의 두 소인수 계수를 결정하는 어려움에 의존합니다. RSA 키 생성은 느리고 키 크기에 따라 시간이 늘어나는 단점이 있습니다.
1985년 처음 제안된 ECC(Elliptic Curve Cryptography)는 비슷한 수준의 보안을 위한 RSA의 키보다 훨씬 작은 키를 사용합니다. 256bit ECC 공개키 보안은 3072bit RSA 공개키와 비슷합니다.
| RSA key size | ECC key size |
|---|---|
| 1024 | 160 |
| 2048 | 244 |
| 3072 | 256 |
| 7680 | 384 |
| 15368 | 512 |
CryptoKit은 ECC알고리즘를 독점적으로 제공합니다. 알고리즘은 NIST의 P256, P384, P521와 Daniel J. Bernstein의 Curve25519을 제공합니다. P256이 가장 널리 사용되는 커브로 prime256v1으로 불리는 OpenSSL의 기본커브 입니다.
Elliptic Curve Cryptography
타원곡선은 아래 방정식을 만족하는 점 (x, y)으로 구성됩니다.
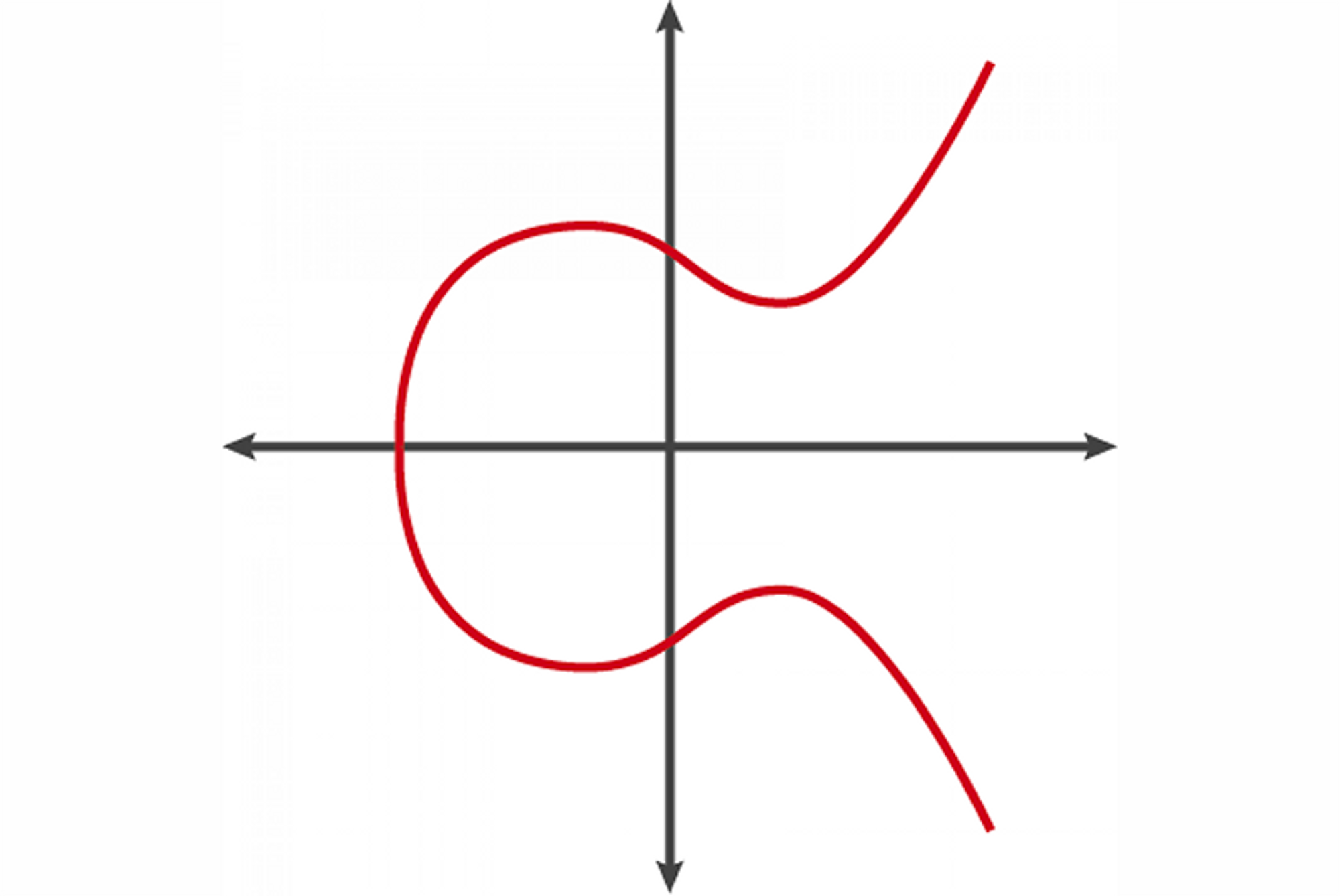
y² = x³ + Ax + B예를 들어, y² = x³ - x + 1은 아래와 같은 타원 곡선 그래프를 그립니다.
ECC는 타원곡선 중 아래 조건을 만족하는 비특이 타원곡선을 사용하는데
4a³ + 27b² ≠ 0ECC는 비특이 타원곡선의 아래와 같은 속성을 이용합니다.
- 그래프는 X축을 중심으로 대칭형
- 수직선이 아닌 모든 선이 그래프와 교차하는 지점은 3개 = 두 점 P와 Q를 연결하는 직선은 반드시 다른 한점과 연결됨
예를 들어 점A와 점B를 연결하는 선을 그립니다. 이 선이 그래프에서 만나는 또다른 점을 X축 대칭으로 반사된 점 C = A•B 를 얻을 수 있는데 이게 타원곡선에서 두 점에 대한 점덧셈연산하는 방법입니다.
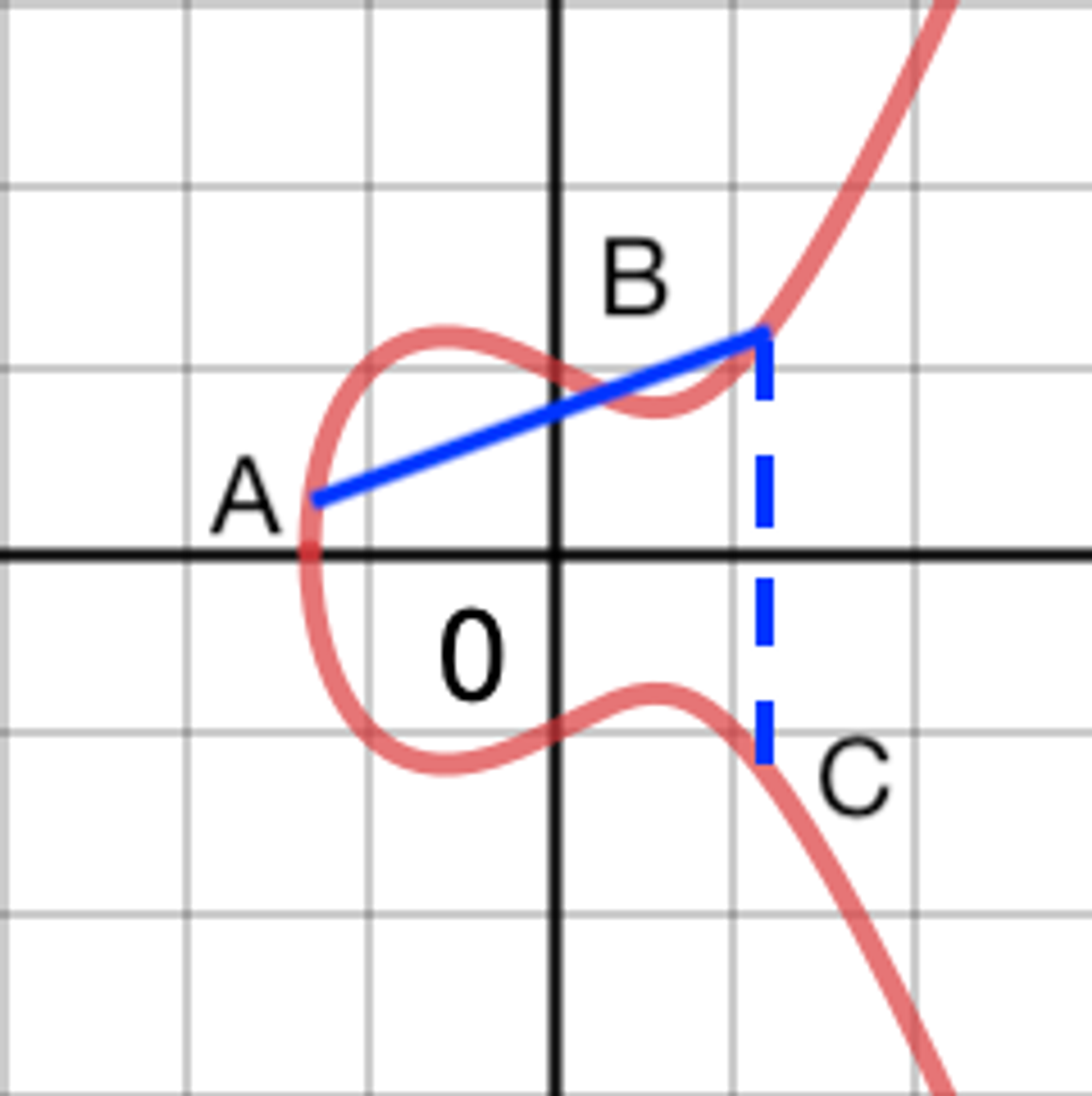
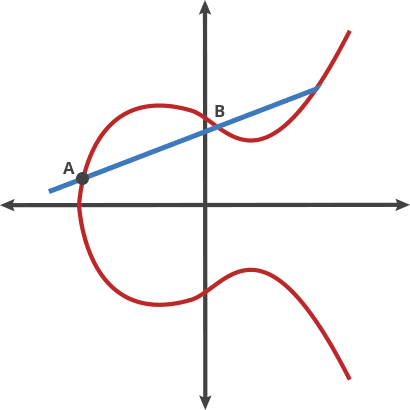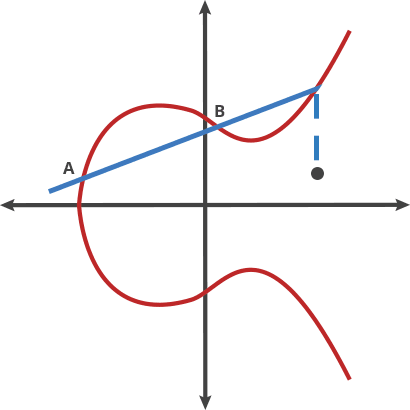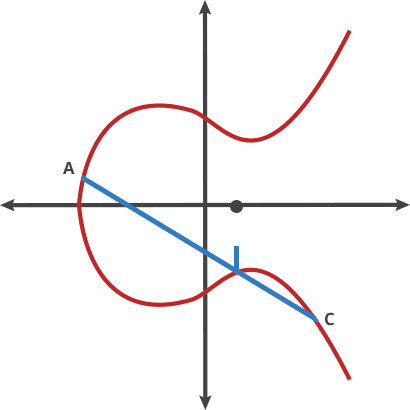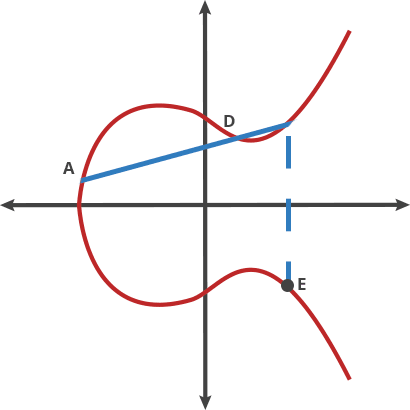
점 P를 2번 연산(P•P)한 경우(= 2•P) 접선(Tangent)과 그래프가 만나는 점을 X축 대칭으로 반사된 점을 구합니다. 이 방법으로 점P에 대한 점곱셈연산을 할 수 있습니다.
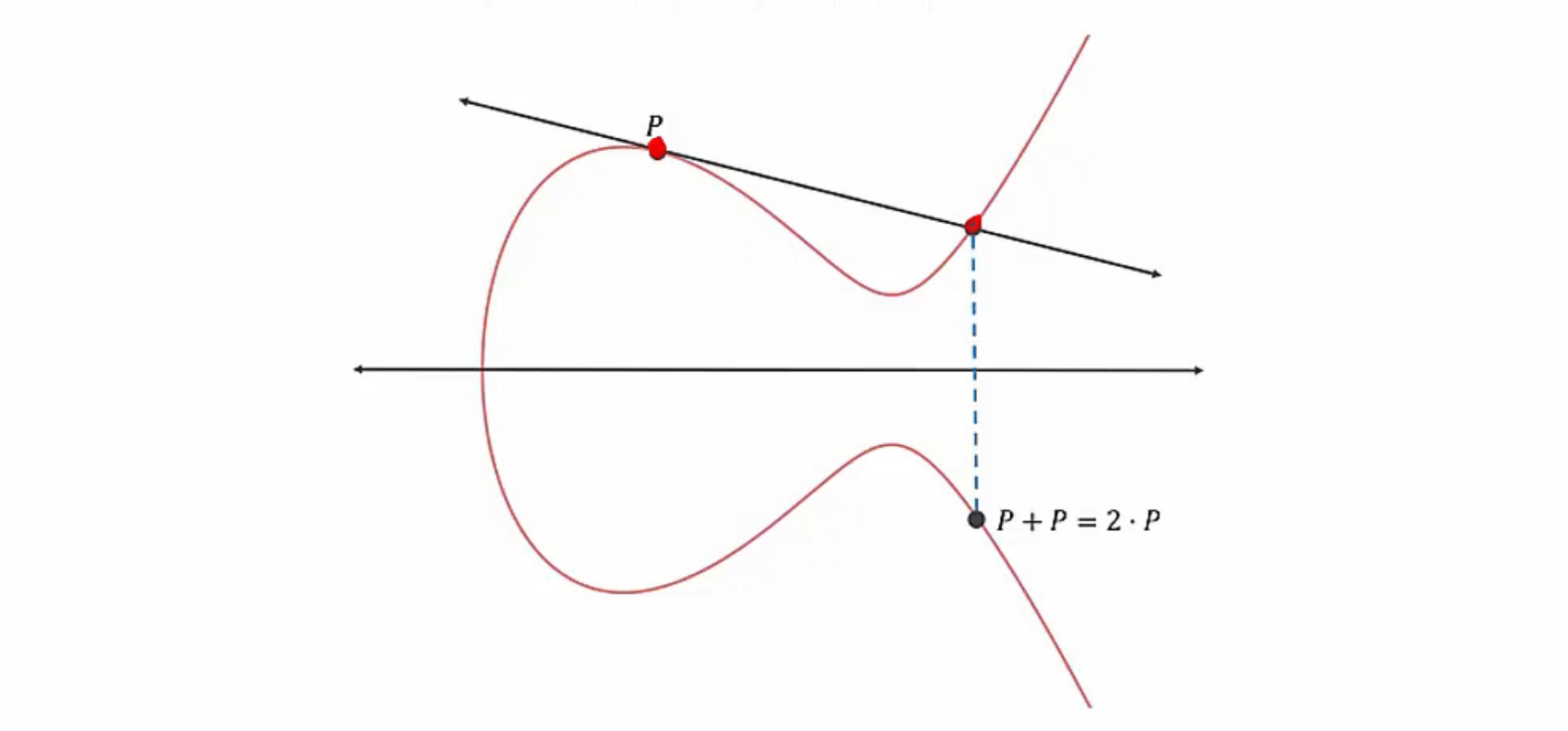
위에서 2P를 통해 구한 점에서 다시 접선을 이용해서 4P를, 다시 반복해서 8P를 구하는 방식으로 배가연산(Doubling)을 할 수 있습니다. 8P•P를 하면 9P가 될 수 있습니다.
아래는 점G의 2G를 구하고, 2G에서 다시 4G를 구하고 4G에서 8G를 구하는 예시입니다.
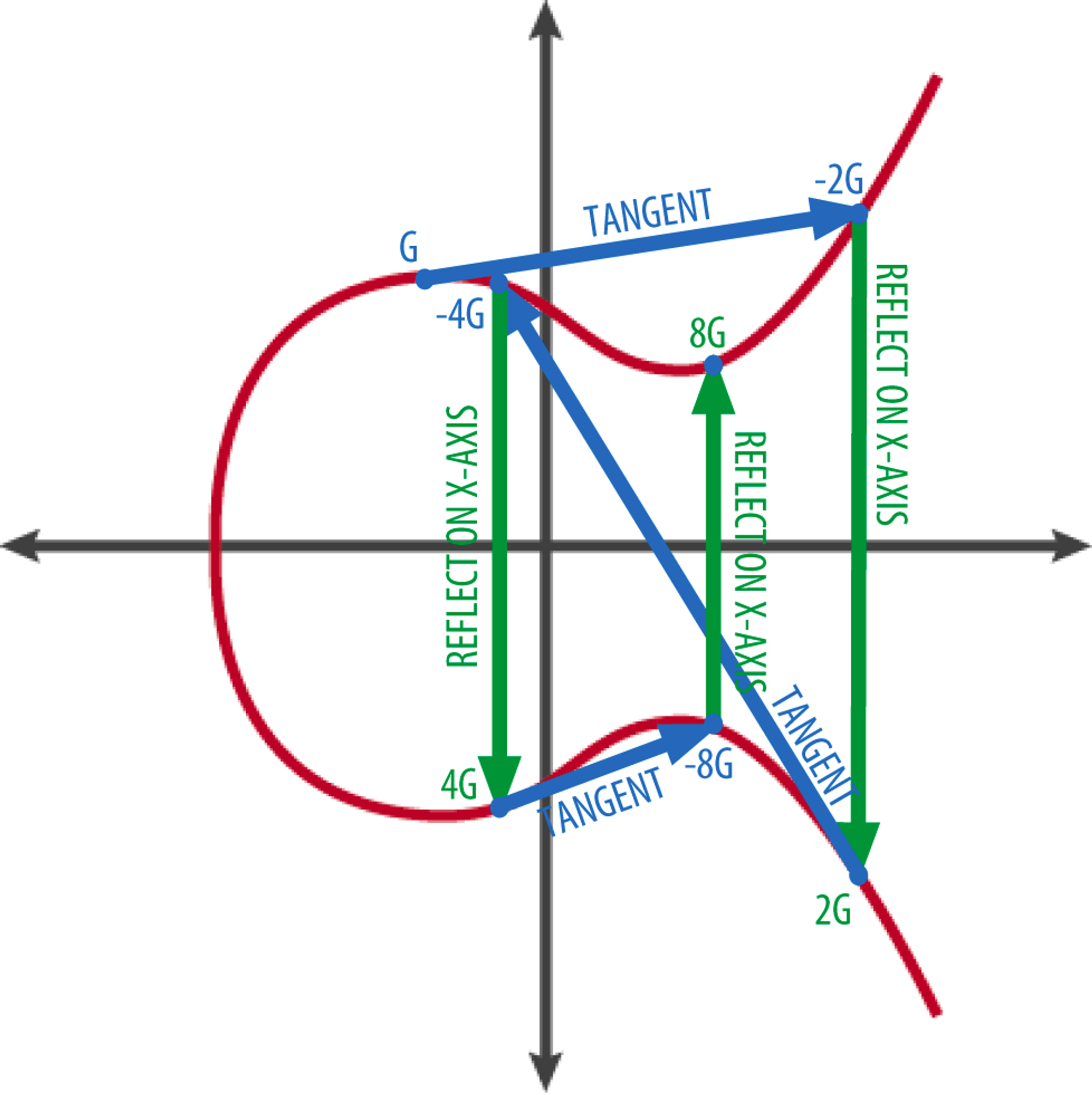
위와 같은 방식으로 점 G에 대한 kG(k는 양수)를 정의합니다. 이 속성을 사용하면 점 G에 대한 k번 점연산한 kG를 매우 빠르게 연산할 수 있습니다.
하지만 거꾸로 점 G와 kG의 정보만으로 k를 연산하는 것은 매우 어렵습니다.
실제 알고리즘은 소수 n을 modulo한 정수 값 x, y만 사용합니다. 시작점은 Generator라고 불러 보통 G라고 칭합니다.
ECC암호화시스템을 설정할 때, 곡선 방정직(계수 x와 상수 b), 이 곡선의 Generator점 G와 그에 해당하는 소수 n을 선택합니다. 그리고 무작위로 선택된 숫자 k가 개인키로 쓰이고, kG연산을 한 점이 공개키로 쓰입니다.
위 연산을 우리가 계산을 할 필요는 없고, Curve25519와 같은 표준곡선, NIST ECC에서 사용하는 곡선이 CryptoKit의 공개키 메서드로 이미 구현이 되어있습니다.
디지털 서명
디지털 서명은 HMAC과 유사하지만 공개키 암호화를 사용합니다. 같은 비밀키로 서명하고 확인하는 대신, Sender는 개인키를 사용해서 서명하고, Receiver는 Sender의 공개키를 사용해서 확인합니다.
(공개키 암호화: 개인키로 서명하고 공개키로 확인)
디지털 서명을 위한 알고리즘에는 2가지가 있습니다.
- NIST의
P256/P384/P512곡선을 사용하는ECDSA(Elliptic Curve Digital Signature Algorithm, 타원곡선 디지털 서명 알고리즘) - BernStein의
Ed25519곡선을 사용하는EdDSA(Edwards-curve Digital Signature Algorithm, 에드워드 곡선 디지털 서명 알고리즘)
Sender가 Receiver에게 본인이 보낸 것을 알 수 있도록 디지털 서명을 하기 위해, 개인키와 공개키를 먼저 만듭니다. 공개키는 네트워크로 보내야 하기 때문에 rawRepresentation으로 Data 타입으로 만들어줍니다.
let senderSigningPrivateKey = Curve25519.Signing.PrivateKey()
let senderSigningPublicKeyData =
senderSigningPrivateKey.publicKey.rawRepresentation
그리고 Sender는 개인키로 Receiver에게 보낼 data에 서명을 합니다.
let signatureForData = try! senderSigningPrivateKey.signature(for: data)
혹은 data의 Digest에 서명을 합니다. data에 서명하는 것보다 빠릅니다.
let digest512 = SHA512.hash(data: data)
let signatureForDigest = try! senderSigningPrivateKey.signature(
for: Data(digest512))
Curve25519 개인키를 사용할 때 signature(for:)는 해시 함수로 SHA-512를 사용해서 Ed25519 타원곡선 위에 data(혹은 Digest)의 EdDSA 서명을 생성합니다. 이 알고리즘은 무작위 nonce를 생성해서 동일한 data와 키에 대해서도 매 호출마다 다른 서명을 생성해서 타이밍 공격을 방지해줍니다.
Curve25519 대신 P256을 사용하는 경우, 해시 함수로 SHA-256을 사용해서 P-256 타원곡선 위에 data의 ECDSA 서명을 생성합니다.
이제 Sender는 Receiver에게 data, digest512와 signatureForData(혹은 signatureForDigest)를 보냅니다.
Receiver는 아래처럼 Sender가 생성한 senderSigningPublicKeyData로 키를 생성해서 서명을 확인할 수 있습니다.
let publicKey = try! Curve25519.Signing.PublicKey(
rawRepresentation: senderSigningPublicKeyData)
if publicKey.isValidSignature(signatureForData, for: data) {
print("Sender가 보낸 데이터가 맞음")
}
if publicKey.isValidSignature(signatureForDigest,
for: Data(digest512)) {
print("보낸 데이터와 받은 데이터가 일치함")
UIImage(data: data) // 데이터 사용
}이제 data를 암호화하는 방법이 남았습니다.
암호화를 위한 대칭키(Symmetric Key) 생성
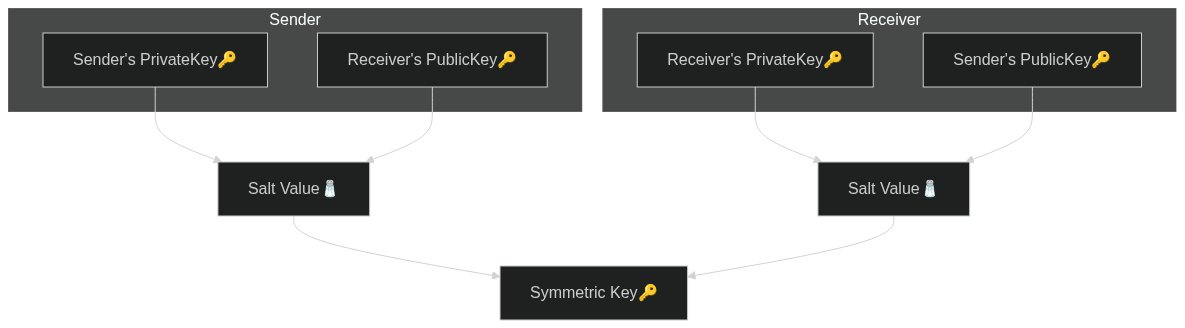
Key agreement algorithm을 사용하면 공개키와 개인키에서 shared secret을 생성한 다음, 합의된 salt value(소금값)을 추가해서 대칭키를 만들 수 있습니다.
Public-Private key agreement algorithm 다이어그램
Shared secret의 생성은 간단합니다.
G = 타원곡선의 생성점, s = Sender의 개인키 라면
s * G가 Sender의 공개키입니다.
마찬가지로 Receiver의 개인키가 r일 때, r * G가 Receiver의 공개키가 됩니다.
Receiver는 Sender의 공개키에 자신의 개인키를 곱하고,
Sender는 Receiver의 공개키에 자신의 개인키를 곱해서 같은 점을 얻을 수 있습니다.
(s * G) * r = (r * G) * s이 방법이 ECDH(Elliptic Curve Diffie Helman) key agreement로,
NIST의 P256/P384/P512 곡선 혹은 Bernstein의 X25519 곡선 중 하나를 사용합니다.
이제 Sender와 Receiver는 key agreement를 위해 개인키와 공개키를 만들고 공개키를 data로 게시합니다.
let senderPrivateKey = Curve25519.KeyAgreement.PrivateKey()
let senderPublicKeyData = senderPrivateKey.publicKey.rawRepresentation
let receiverPrivateKey = Curve25519.KeyAgreement.PrivateKey()
let receiverPublicKeyData = receiverPrivateKey.publicKey.rawRepresentation
Sender와 Receiver는 대칭키를 만들기 위한 salt value에 agree(동의)해야 합니다.
이 salt value는 네트워크로 전송해도 상관없습니다. 공격자가 개인키 중 하나를 알고 있지 않는 한 공격자가 쓸 수 없습니다.
let protocolSalt = "둘이 약속한 소금값".data(using: .utf8)!
Sender는 Receiver의 공개키를 raw representation으로 생성하고, 이를 개인키와 결합해서 먼저 sharedSecret을 계산한 다음 대칭키를 계산합니다.
let receiverPublicKey = try! Curve25519.KeyAgreement.PublicKey(
rawRepresentation: receiverPublicKeyData)
let senderSharedSecret = try! senderPrivateKey.sharedSecretFromKeyAgreement(
with: receiverPublicKey)
let senderSymmetricKey = senderSharedSecret.hkdfDerivedSymmetricKey(
using: SHA256.self, salt: protocolSalt,
sharedInfo: Data(), outputByteCount: 32)
Receiver는 raw representation에서 Sender의 공개키를 생성하고, 이를 자신의 개인키와 결합해서 sharedSecret을 계산하고 대칭키를 계산합니다.
let senderPublicKey = try! Curve25519.KeyAgreement.PublicKey(
rawRepresentation: senderPublicKeyData)
let receiverSharedSecret = try! receiverPrivateKey.sharedSecretFromKeyAgreement(
with: senderPublicKey)
let receiverSymmetricKey = receiverSharedSecret.hkdfDerivedSymmetricKey(
using: SHA256.self, salt: protocolSalt,
sharedInfo: Data(), outputByteCount: 32)
두 대칭키가 일치하는지 확인해볼 수 있습니다.
if senderSymmetricKey == receiverSymmetricKey {
print("Sender와 Receiver의 대칭키가 일치!")
}이제 Sender와 Receiver는 동일한 대칭키를 생성할 수 있고, 이 대칭키로 AEAD authenticated encryption에 사용할 수 있게 됩니다.
(AEAD authenticated encryption하는 방법은 이전글 참고)
Secure Enclave의 P256 Key
추가적인 보호를 위해 Secure Enclave에서 직접 P256 개인키를 생성할 수 있습니다.
// Secure Enclave 사용한 디바이스인지 체크
if SecureEnclave.isAvailable {
// Secure Enclave에서 P256 개인키 생성
let privateKey = try SecureEnclave.P256.Signing.PrivateKey()
} else {
let privateKey = P256.Signing.PrivateKey()
}
Secure Enclave에서 개인키를 사용하면 공개키 데이터를 생성하고 data, Digest에 서명하는 작업은 기존과 동일합니다.
// 개인키 data 생성
let publicKeyData = privateKey.publicKey.compactRepresentation!
// 서명 생성
let dataSignature = try privateKey.signature(for: data)
let digestSignature = try privateKey.signature(for: digest)
Secure Enclave에서는 Access Control을 통해 키 사용을 제한할 수 있습니다.
예를 들어 아래와 같이 작성하면 Secure Enclave에서 생성하는 키를 디바이스의 잠금이 해제된 경우에만 접근 할 수 있고, 해당 디바이스에서만 접근할 수 있도록 접근제한을 설정할 수 있습니다(kSecAttrAccessibleWhenUnlockedThisDeviceOnly). 그리고 개인키로 작업을 수행할 때 사용자의 존재를 요구하도록 하는데 이는 사용자가 TouchID, FaceID 혹은 디바이스 암호로 인증을 해야함을 의미합니다([.privateKeyUsage, .userPresence]).
let accessControl = SecAccessControlCreateWithFlags(
nil,
kSecAttrAccessibleWhenUnlockedThisDeviceOnly,
[.privateKeyUsage, .userPresence],
nil)!
let privateKey = try SecureEnclave.P256.Signing.PrivateKey(
accessControl: accessControl)
Public-Key Cryptography
이전 글에서 정리했던 HMAC, Sealed Box암호화는 Sender와 Receiver모두 키를 알고 있는 대칭키를 사용합니다.
대칭키는 대역 외(Out of band)로 전송되어야 하고, 이 작업을 안전하게 수행할 수 없는 경우 공개키 암호화(public-key cryptography)를 사용합니다. 실제로 인터넷에서 일상적으로 사용하는 대부분의 암호화는 공개키 암호화를 사용하고, Xcode가 앱에 서명을 할 때에도 동일합니다.
공개키 암호화는 수학적으로 연결된 두개의 키를 생성합니다. 개인키는 비밀로 유지하고 해당 공개키 Data를 게시합니다. 개인키로 Data 혹은 Data Digest에 서명한 다음 전송합니다. Receiver는 공개키 Data에서 공개키를 생성한 다음 이를 사용하여 Signed Data 혹은 Digest를 확인합니다.
예를 들어, 앱에서 백엔드 서버로 작업을 인증해야 할 수 있습니다. 사용자 디바이스에서 개인키를 생성해서 Keychain 혹은 SecureEnclave에 저장한 다음, 해당 공개키를 서버에 등록합니다. 사용자가 작업을 설정하면 앱이 사용자의 개인키로 작업 세부정보에 서명하고 서명된 세부정보를 서버로 전송하면 서버가 사용자의 공개키로 이를 확인합니다.
Encrypted data를 전송하려면 사용자와 Receiver가 각각 키 쌍을 생성하고 공개키를 게시합니다. 그리고 사용자, Receiver 모두 자신의 개인키와 상대방의 공개키를 결합해서 shared secret을 생성합니다. 양쪽 모두 이 shared secret을 사용하여 동일한 대칭키를 만들어낸 다음 위에서 설명했던 AEAD에 사용할 수 있습니다.
개인키, 공개키 생성하기
공개키 암호화의 주요 특징은 Trapdoor 알고리즘을 사용한다는 점입니다. 공개키로부터 개인키를 계산해내는 것은 매우 어렵습니다.
1978년 RSA(Rivest-Shamir-Adleman)가 발표된 후 가장 널리 사용되는 공개키 알고리즘이 되었습니다. RSA 알고리즘은 매우매우 큰 수의 두 소인수 계수를 결정하는 어려움에 의존합니다. RSA 키 생성은 느리고 키 크기에 따라 시간이 늘어나는 단점이 있습니다.
1985년 처음 제안된 ECC(Elliptic Curve Cryptography)는 비슷한 수준의 보안을 위한 RSA의 키보다 훨씬 작은 키를 사용합니다. 256bit ECC 공개키 보안은 3072bit RSA 공개키와 비슷합니다.
| RSA key size | ECC key size |
|---|---|
| 1024 | 160 |
| 2048 | 244 |
| 3072 | 256 |
| 7680 | 384 |
| 15368 | 512 |
CryptoKit은 ECC알고리즘를 독점적으로 제공합니다. 알고리즘은 NIST의 P256, P384, P521와 Daniel J. Bernstein의 Curve25519을 제공합니다. P256이 가장 널리 사용되는 커브로 prime256v1으로 불리는 OpenSSL의 기본커브 입니다.
Elliptic Curve Cryptography
타원곡선은 아래 방정식을 만족하는 점 (x, y)으로 구성됩니다.
y² = x³ + Ax + B예를 들어, y² = x³ - x + 1은 아래와 같은 타원 곡선 그래프를 그립니다.

ECC는 타원곡선 중 아래 조건을 만족하는 비특이 타원곡선을 사용하는데
4a³ + 27b² ≠ 0ECC는 비특이 타원곡선의 아래와 같은 속성을 이용합니다.
- 그래프는 X축을 중심으로 대칭형
- 수직선이 아닌 모든 선이 그래프와 교차하는 지점은 3개 = 두 점 P와 Q를 연결하는 직선은 반드시 다른 한점과 연결됨
예를 들어 점A와 점B를 연결하는 선을 그립니다. 이 선이 그래프에서 만나는 또다른 점을 X축 대칭으로 반사된 점 C = A•B 를 얻을 수 있는데 이게 타원곡선에서 두 점에 대한 점덧셈연산하는 방법입니다.


점 P를 2번 연산(P•P)한 경우(= 2•P) 접선(Tangent)과 그래프가 만나는 점을 X축 대칭으로 반사된 점을 구합니다. 이 방법으로 점P에 대한 점곱셈연산을 할 수 있습니다.

위에서 2P를 통해 구한 점에서 다시 접선을 이용해서 4P를, 다시 반복해서 8P를 구하는 방식으로 배가연산(Doubling)을 할 수 있습니다. 8P•P를 하면 9P가 될 수 있습니다.
아래는 점G의 2G를 구하고, 2G에서 다시 4G를 구하고 4G에서 8G를 구하는 예시입니다.

위와 같은 방식으로 점 G에 대한 kG(k는 양수)를 정의합니다. 이 속성을 사용하면 점 G에 대한 k번 점연산한 kG를 매우 빠르게 연산할 수 있습니다.
하지만 거꾸로 점 G와 kG의 정보만으로 k를 연산하는 것은 매우 어렵습니다.
실제 알고리즘은 소수 n을 modulo한 정수 값 x, y만 사용합니다. 시작점은 Generator라고 불러 보통 G라고 칭합니다.
ECC암호화시스템을 설정할 때, 곡선 방정직(계수 x와 상수 b), 이 곡선의 Generator점 G와 그에 해당하는 소수 n을 선택합니다. 그리고 무작위로 선택된 숫자 k가 개인키로 쓰이고, kG연산을 한 점이 공개키로 쓰입니다.
위 연산을 우리가 계산을 할 필요는 없고, Curve25519와 같은 표준곡선, NIST ECC에서 사용하는 곡선이 CryptoKit의 공개키 메서드로 이미 구현이 되어있습니다.
디지털 서명
디지털 서명은 HMAC과 유사하지만 공개키 암호화를 사용합니다. 같은 비밀키로 서명하고 확인하는 대신, Sender는 개인키를 사용해서 서명하고, Receiver는 Sender의 공개키를 사용해서 확인합니다.
(공개키 암호화: 개인키로 서명하고 공개키로 확인)
디지털 서명을 위한 알고리즘에는 2가지가 있습니다.
- NIST의
P256/P384/P512곡선을 사용하는ECDSA(Elliptic Curve Digital Signature Algorithm, 타원곡선 디지털 서명 알고리즘) - BernStein의
Ed25519곡선을 사용하는EdDSA(Edwards-curve Digital Signature Algorithm, 에드워드 곡선 디지털 서명 알고리즘)
Sender가 Receiver에게 본인이 보낸 것을 알 수 있도록 디지털 서명을 하기 위해, 개인키와 공개키를 먼저 만듭니다. 공개키는 네트워크로 보내야 하기 때문에 rawRepresentation으로 Data 타입으로 만들어줍니다.
let senderSigningPrivateKey = Curve25519.Signing.PrivateKey()
let senderSigningPublicKeyData =
senderSigningPrivateKey.publicKey.rawRepresentation
그리고 Sender는 개인키로 Receiver에게 보낼 data에 서명을 합니다.
let signatureForData = try! senderSigningPrivateKey.signature(for: data)
혹은 data의 Digest에 서명을 합니다. data에 서명하는 것보다 빠릅니다.
let digest512 = SHA512.hash(data: data)
let signatureForDigest = try! senderSigningPrivateKey.signature(
for: Data(digest512))
Curve25519 개인키를 사용할 때 signature(for:)는 해시 함수로 SHA-512를 사용해서 Ed25519 타원곡선 위에 data(혹은 Digest)의 EdDSA 서명을 생성합니다. 이 알고리즘은 무작위 nonce를 생성해서 동일한 data와 키에 대해서도 매 호출마다 다른 서명을 생성해서 타이밍 공격을 방지해줍니다.
Curve25519 대신 P256을 사용하는 경우, 해시 함수로 SHA-256을 사용해서 P-256 타원곡선 위에 data의 ECDSA 서명을 생성합니다.
이제 Sender는 Receiver에게 data, digest512와 signatureForData(혹은 signatureForDigest)를 보냅니다.
Receiver는 아래처럼 Sender가 생성한 senderSigningPublicKeyData로 키를 생성해서 서명을 확인할 수 있습니다.
let publicKey = try! Curve25519.Signing.PublicKey(
rawRepresentation: senderSigningPublicKeyData)
if publicKey.isValidSignature(signatureForData, for: data) {
print("Sender가 보낸 데이터가 맞음")
}
if publicKey.isValidSignature(signatureForDigest,
for: Data(digest512)) {
print("보낸 데이터와 받은 데이터가 일치함")
UIImage(data: data) // 데이터 사용
}이제 data를 암호화하는 방법이 남았습니다.
암호화를 위한 대칭키(Symmetric Key) 생성
Key agreement algorithm을 사용하면 공개키와 개인키에서 shared secret을 생성한 다음, 합의된 salt value(소금값)을 추가해서 대칭키를 만들 수 있습니다.
Public-Private key agreement algorithm 다이어그램
Shared secret의 생성은 간단합니다.
G = 타원곡선의 생성점, s = Sender의 개인키 라면
s * G가 Sender의 공개키입니다.
마찬가지로 Receiver의 개인키가 r일 때, r * G가 Receiver의 공개키가 됩니다.
Receiver는 Sender의 공개키에 자신의 개인키를 곱하고,
Sender는 Receiver의 공개키에 자신의 개인키를 곱해서 같은 점을 얻을 수 있습니다.
(s * G) * r = (r * G) * s이 방법이 ECDH(Elliptic Curve Diffie Helman) key agreement로,
NIST의 P256/P384/P512 곡선 혹은 Bernstein의 X25519 곡선 중 하나를 사용합니다.
이제 Sender와 Receiver는 key agreement를 위해 개인키와 공개키를 만들고 공개키를 data로 게시합니다.
let senderPrivateKey = Curve25519.KeyAgreement.PrivateKey()
let senderPublicKeyData = senderPrivateKey.publicKey.rawRepresentation
let receiverPrivateKey = Curve25519.KeyAgreement.PrivateKey()
let receiverPublicKeyData = receiverPrivateKey.publicKey.rawRepresentation
Sender와 Receiver는 대칭키를 만들기 위한 salt value에 agree(동의)해야 합니다.
이 salt value는 네트워크로 전송해도 상관없습니다. 공격자가 개인키 중 하나를 알고 있지 않는 한 공격자가 쓸 수 없습니다.
let protocolSalt = "둘이 약속한 소금값".data(using: .utf8)!
Sender는 Receiver의 공개키를 raw representation으로 생성하고, 이를 개인키와 결합해서 먼저 sharedSecret을 계산한 다음 대칭키를 계산합니다.
let receiverPublicKey = try! Curve25519.KeyAgreement.PublicKey(
rawRepresentation: receiverPublicKeyData)
let senderSharedSecret = try! senderPrivateKey.sharedSecretFromKeyAgreement(
with: receiverPublicKey)
let senderSymmetricKey = senderSharedSecret.hkdfDerivedSymmetricKey(
using: SHA256.self, salt: protocolSalt,
sharedInfo: Data(), outputByteCount: 32)
Receiver는 raw representation에서 Sender의 공개키를 생성하고, 이를 자신의 개인키와 결합해서 sharedSecret을 계산하고 대칭키를 계산합니다.
let senderPublicKey = try! Curve25519.KeyAgreement.PublicKey(
rawRepresentation: senderPublicKeyData)
let receiverSharedSecret = try! receiverPrivateKey.sharedSecretFromKeyAgreement(
with: senderPublicKey)
let receiverSymmetricKey = receiverSharedSecret.hkdfDerivedSymmetricKey(
using: SHA256.self, salt: protocolSalt,
sharedInfo: Data(), outputByteCount: 32)
두 대칭키가 일치하는지 확인해볼 수 있습니다.
if senderSymmetricKey == receiverSymmetricKey {
print("Sender와 Receiver의 대칭키가 일치!")
}이제 Sender와 Receiver는 동일한 대칭키를 생성할 수 있고, 이 대칭키로 AEAD authenticated encryption에 사용할 수 있게 됩니다.
(AEAD authenticated encryption하는 방법은 이전글 참고)
Secure Enclave의 P256 Key
추가적인 보호를 위해 Secure Enclave에서 직접 P256 개인키를 생성할 수 있습니다.
// Secure Enclave 사용한 디바이스인지 체크
if SecureEnclave.isAvailable {
// Secure Enclave에서 P256 개인키 생성
let privateKey = try SecureEnclave.P256.Signing.PrivateKey()
} else {
let privateKey = P256.Signing.PrivateKey()
}
Secure Enclave에서 개인키를 사용하면 공개키 데이터를 생성하고 data, Digest에 서명하는 작업은 기존과 동일합니다.
// 개인키 data 생성
let publicKeyData = privateKey.publicKey.compactRepresentation!
// 서명 생성
let dataSignature = try privateKey.signature(for: data)
let digestSignature = try privateKey.signature(for: digest)
Secure Enclave에서는 Access Control을 통해 키 사용을 제한할 수 있습니다.
예를 들어 아래와 같이 작성하면 Secure Enclave에서 생성하는 키를 디바이스의 잠금이 해제된 경우에만 접근 할 수 있고, 해당 디바이스에서만 접근할 수 있도록 접근제한을 설정할 수 있습니다(kSecAttrAccessibleWhenUnlockedThisDeviceOnly). 그리고 개인키로 작업을 수행할 때 사용자의 존재를 요구하도록 하는데 이는 사용자가 TouchID, FaceID 혹은 디바이스 암호로 인증을 해야함을 의미합니다([.privateKeyUsage, .userPresence]).
let accessControl = SecAccessControlCreateWithFlags(
nil,
kSecAttrAccessibleWhenUnlockedThisDeviceOnly,
[.privateKeyUsage, .userPresence],
nil)!
let privateKey = try SecureEnclave.P256.Signing.PrivateKey(
accessControl: accessControl)